最近着手于机器学习，但是苦于已将数学知识还给了老师多年，看着满屏的数学公式尤为头疼。 还好看了一篇关于卷积神经网络的数学基础以后，发现慢慢的可以看懂一些东西了，这里也记录一下自己的所学，千里之行始于足下，先从最基础的开学学习。

常用的概念

• 标量：可以理解为标量就是一个单独的数，如，1，2，3等
• 向量：一个向量是一列数。这些数是有序排列的。如[1,2,3,4]
• 矩阵：可以理解为一张二维的数据表，它由m*n(m行n列)组成
• 张量：超过两维的数组，三维还可以想象成一个立体，超过三维就不好比喻了。

numpy中的表示矩阵

向量,直接使用numpy.array([1,2,3])来表示 矩阵，矩阵是二维的数组，可以使用numpy.array([[1,2],[3,4],[5,6]]) 张量：使用numpy.array([[[1,2],[3,4]],[[5,6],[7,8]],[[9,10],[11,12]]])

>>> import numpy as np
>>> a = np.array([1,2,3])
>>> b = np.array([[1,2],[3,4],[5,6]])
>>> c = np.array([[[1,2],[3,4]],[[5,6],[7,8]],[[9,10],[11,12]]])
>>> print(a)
[1 2 3]
>>> print(b)
[[1 2]
 [3 4]
 [5 6]]
>>> print(c)
[[[ 1  2]
  [ 3  4]]

 [[ 5  6]
  [ 7  8]]

 [[ 9 10]
  [11 12]]]

以下主要以二维的矩阵作来讨论

矩阵的运算

矩阵与标量进行运算

是以矩阵上每个元素和标量进行运算

>>> a  = np.array([[1,2],[3,4],[5,6]])
>>> a
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> a+1
array([[2, 3],
       [4, 5],
       [6, 7]])
>>> a-1
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> a*2
array([[ 2,  4],
       [ 6,  8],
       [10, 12]])
>>> a/2
array([[0.5, 1. ],
       [1.5, 2. ],
       [2.5, 3. ]])

矩阵与向量进行加减运算

首先明确一下，不是所有的向量都能和矩阵进行运算，它和矩阵的shape有关,上面定义的a，它的shape是(3,2),表示有3行2列，如果想要和向量做加减，只要保证向量里元素的个数等于矩阵的列数即可

>>> a
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> e
array([10, 20, 30])
>>> d
array([10, 20])
>>> a+d
array([[11, 22],
       [13, 24],
       [15, 26]])
>>> a+e
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (3,2) (3,)

最后a+e的操作，a是(3,2)的矩阵，e是有3个元素的向量，不能进行相加操作

矩阵与向量相乘

这里的相乘分为两种情况，一种是使用*运算符，一种是使用np.dot(),称为点积. 先普通的乘积，它的规则和相加减是一样的，需要向量的元素数里等于矩阵的列数，对应位置的数进行相乘操作

>>> a
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> b = np.array([2,4])
>>> a*b
array([[ 2,  8],
       [ 6, 16],
       [10, 24]])

对于点积，这里需要考虑向量是乘数还是被乘数，就是向量是在乘号左边还是右边，当向量在操作符的左边时，需要满足向量元素的个数等于矩阵的**行数**，得到的结果是向量，它的元素数量为矩阵行列数，当向量在操作符右边时，需要满足向量的元素数量为矩阵的**列数**,得到一个向量，它的元素个数为矩阵的行数。说起来比较绕，看下面的例子

>>> a
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> a.shape
(3, 2)
>>> b = np.array([1,2,3])
>>> c = np.array([10,20])
>>> np.dot(a,b)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: shapes (3,2) and (3,) not aligned: 2 (dim 1) != 3 (dim 0)
>>> np.dot(b,a)
array([22, 28])
>>> np.dot(a,c)
array([ 50, 110, 170])
>>> np.dot(c,a)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: shapes (2,) and (3,2) not aligned: 2 (dim 0) != 3 (dim 0)

a是一个3x2的矩阵，b是一个有3个元素的向量，c有2个元素。 当用a点积b时，由于b的元素数量不等于a的列数，所以它们不能做点积运算。下面的和c做点积运算同理.

再来看下点积是怎么算出来的 np.dot(b,a),按照上面所说，它应该得到一个有两个元素的向量，向量3点乘(3,2) 得到有2个元素的向量 先把矩阵按列分为[1,3,5]和[2,4,6],然后向量b [1,2,3] 分别和拆分后的矩阵进行相乘并加和，也就是 [1*1+3*2+5*3,2*1+4*2+6*3] 得到[22,28]

当向量在点积右边的时候，矩阵a(3,2) 点乘向量c(2,) 得到一个有3个元素的向量，这次要把矩阵按照行来拆分成[1,2],[3,4],[5,6],然后分别和c[10,20] 进行相乘相加 [1*10+2*20,3*10+4*20,5*10+6*20] 得到[50,110,170]

这里比较迷惑的就是矩阵什么是按行分还是按列分。

矩阵与矩阵的相乘

两个矩阵如果想要使用* 相乘的话，需要满足两种条件之一即可 1. 两个矩阵的shape是一样的，比如都是3x2的 2. 如其中一个矩阵是3x2,则另外一个矩阵可以是(1x2)或者(3x1) 另外一个矩阵可以是一行二列或者三行一列

对于第一种情况，会将两个矩阵对应的数相乘，得到新的矩阵

>>> a
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> c
array([[10, 20],
       [30, 40],
       [50, 60]])
>>> a*c
array([[ 10,  40],
       [ 90, 160],
       [250, 360]])

对于第二种情况，直接看下面的输出吧

>>> d
array([[10, 20]]) #d是(1x2) 的
>>> e # e是(3x1) 的
array([[10],
       [20],
       [30]])
>>> a #a是（3*2）的
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> a*d
array([[ 10,  40],
       [ 30,  80],
       [ 50, 120]])
>>> a*e
array([[ 10,  20],
       [ 60,  80],
       [150, 180]])
>>>

矩阵的点积

先看一张图

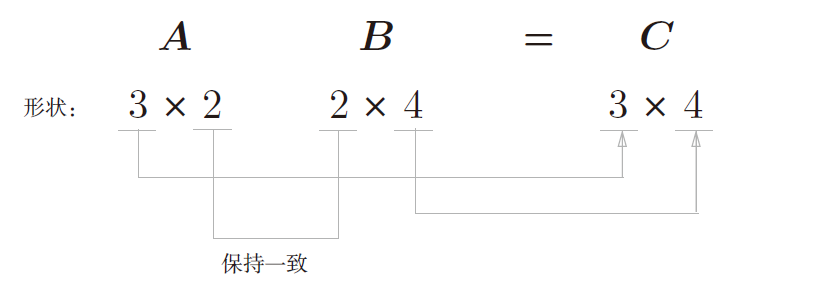
这张图说明了，两个矩阵可以做点积的条件，A的列数要等于B的行数，点积结果的行由A决定，列由B决定，所以通过情况下，A点积B 和B点积A 会得到不同的结果

点击的运算规则如下图

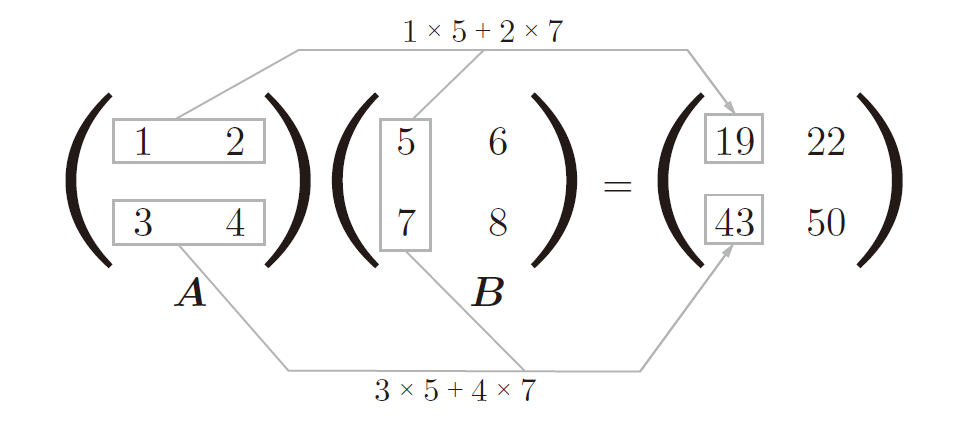
>>> a
array([[1, 2],
       [3, 4],
       [5, 6]])
>>> b
array([[10, 20, 30],
       [40, 50, 60]])
>>> np.dot(a,b)
array([[ 90, 120, 150],
       [190, 260, 330],
       [290, 400, 510]])
>>> np.dot(b,a)
array([[220, 280],
       [490, 640]])

以上就是关于矩阵的相关运算，看着比较让人头疼，不过看多了算熟了记下规则即可，numpy库在做关于矩阵的运算非常方便.