跳转至

神经网络中常见激活函数的python表达

在神经网络最后的输出层，通常会使用激活函数将最后一层神经元得到的数据再进行计算，最终得到一个输出的结果，这里称该函数为激活函数，比对输出表达式为，当最后一层输出元得到的数据大于0，则输出1，小于0则输出0，这种称为阶跃函数，常见的激活函数有阶跃函数，sigmoid，ReLU，tanh函数

阶跃函数

阶跃函数的意义为，当输入数据大于某个值时输出值A，小于等于某个值时为B，表现为在某个值时输出突然变化，数学表达为 阶跃函数

该图表示，当输入小于等于0时，输出0，大于0时输出1，使用python的函数表达为

1
2
3
4
5
def step_function(x):
    if x > 0:
        return 1
    else:
        return 0
函数比较简单，但是通常情况下，我们输入的数一般不会只是简单的一个数，一般是一个向量，将上面的函数使用numpy模块进行一下改造。 
1
2
3
4
5
6
7
import numpy as np

def step_function(x):
    y = x>0
    return y.astype(np.int)

print(step_function(np.array([1.0,2.0,0,-2.3])))
上面脚本的输出为[1 1 0 0]

y=x>0 利用numpy的广播功能，将numpy数组依次和0进行对比，当大于0的时候返回True，否则返回False,再将True和False转换为int的0和1 

1
2
3
4
5
6
7
>>> import numpy as np
>>> x = np.array([1.0,2.0,0,-2.3])
>>> y = x>0
>>> y
array([ True,  True, False, False])
>>> y.astype(np.int)
array([1, 1, 0, 0])

如果使用matplotlib对上面的函数进行图形化展示，如下 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
#coding:utf-8

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
    y = x>0
    return y.astype(np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

得到的图形如下 阶跃图形

sigmoid函数

阶跃函数在行为上表现的过于激进，更多的情况下我们希望在神经网络中得到一种更为平滑的输出，由其在分类问题中，比如我们一共可能有5种输出结果，我们希望在最后的激活函数中得到这5种结果的概率，取概率最大的那种可能结果，这时我们就不希望用到上面这种过于激进的函数，我们可以使用sigmoid函数。

sigmoid函数的数学表达式为

sigmoid表达式

其中exp(−x)表示 e^{-x} 的意思。e是纳皮尔常数2.7182...

python 的函数表达为 

1
2
3
4
5
6
7
8
#coding:utf-8

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

print(sigmoid(np.array([-2.0,1.0,2.0])))

输出为[0.11920292 0.73105858 0.88079708]

sigmoid的函数图形为

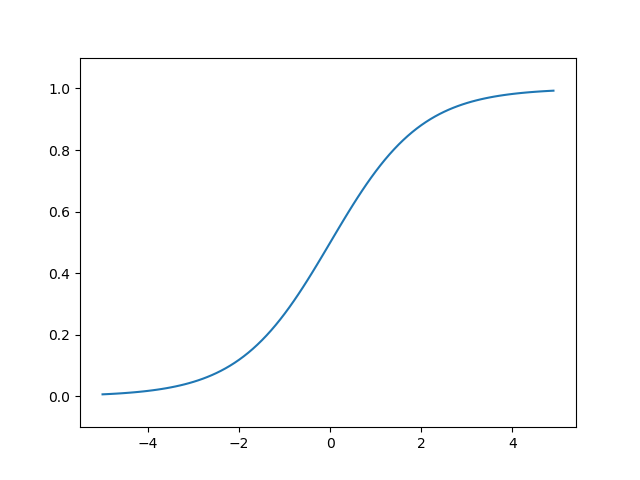
sigmoid图形

将sigmoid函数与阶跃函数放在一起 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
#coding:utf-8

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
    y = x>0
    return y.astype(np.int)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))


print(sigmoid(np.array([-2.0,1.0,2.0])))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
ys = step_function(x)
plt.plot(x, y)
plt.plot(x, ys)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()
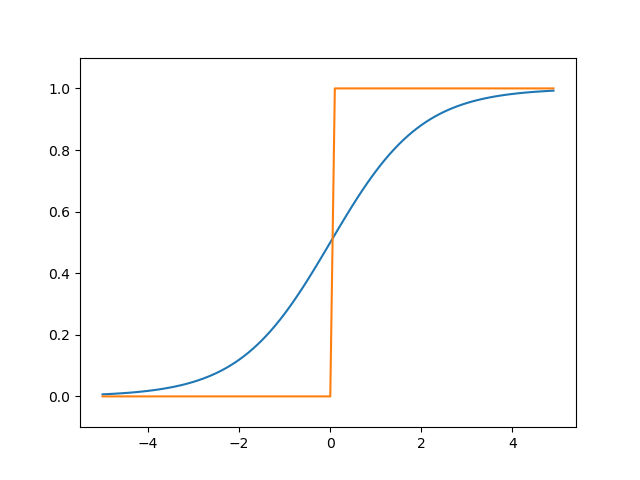
sigmoid与阶跃图形对比

可以看出sigmoid函数比阶跃函数要平滑。

tanh函数

tanh的数学表达式为 tanh

表现为输入从-10到10之间，输出会从-1到1之间平滑变化，大于10的输出1，小于-10的输出-1，

python函数表达为 

1
2
3
4
def tanh(x):
    return np.true_divide(np.exp(x) - np.exp(-x),np.exp(x) + np.exp(-x))

print(tanh(np.array([-11,-10,-9,-2.0,0,2.0,3.0,10.0,11.2])))
上面输出为 
1
2
[-1.         -1.         -0.99999997 -0.96402758  0.          0.96402758
  0.99505475  1.          1.        ]

tanh的图形为 tanh

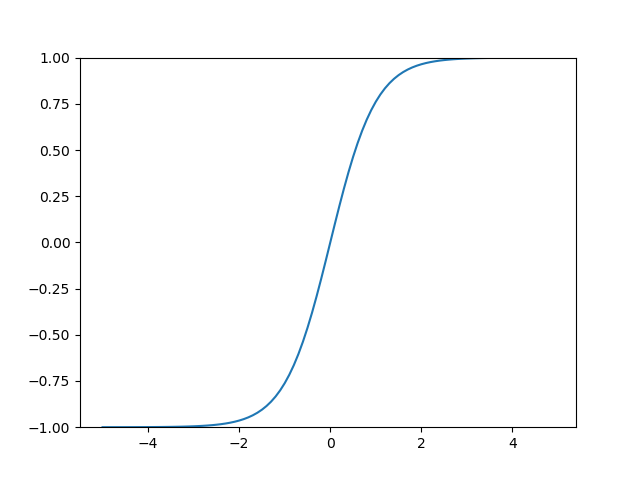
ReLU函数

ReLU函数在输入大于0 时，直接输出该值；在输入小于等于0 时，输出0，数学表达式为

sigmoid与阶跃图形对比

ReLU的python表达式为 

1
2
3
4
def relu(x):
    return np.maximum(0,x)

print(relu(np.array([-2.0,1.0,2.0])))
输出为[0. 1. 2.]

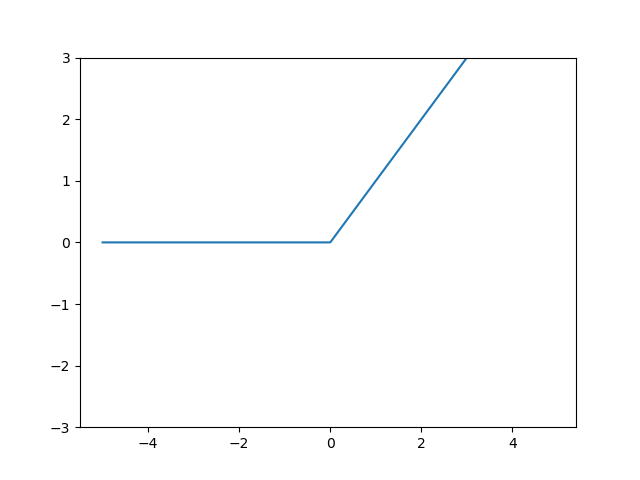
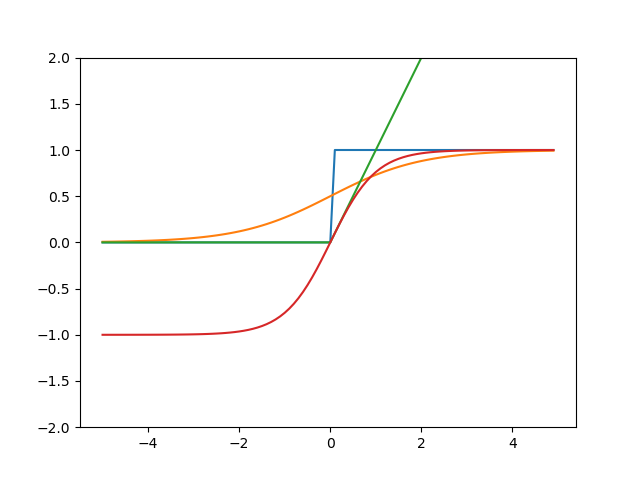
ReLU的图形为 ReLU图形

上面四个激活函数的图形放到一起为 ReLU图形

参考资料 《深度学习入门：基于Python的理论与实现》